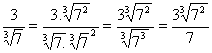Simplificação de expressões com radicais
Nas expressões que contém radicais, efetuamos os cálculos seguindo esta ordem:
1° as operações entre parênteses ( );
2° as operações entre colchetes [ ];
3° as operações entre chaves { }
Entre os parênteses, os colchetes ou as chaves, podem aparecer as operações de adição, subtração, multiplicação, divisão, potenciação e radiciação. A ordem em que as operações devem ser efetuadas é:
1° potenciação e radiciação
2° multiplicação e divisão
3° adição e subtração
Potência com expoente fracionário
O expoente de uma potência pode ser um número em forma de fração.
Exemplo:
.png)
Podemos escrever este número em forma de uma raiz quadrada (pois o denominador da fração é 2).
.png)
Note que quando escrevemos um número com potência fracionária, teremos a seguinte propriedade:
O numerador da potência corresponde ao expoente do número que está na base.
O denominador da potência corresponde ao grau da raiz. No nosso caso é uma raiz de grau 3 (raiz cúbica).
Fazer essa transformação de um número em uma raiz para um número com potência fracionária nos auxilia quando queremos multiplicar números de mesma base, porém em raízes de graus diferentes.
Exemplo:
.png)
Equação do 2° grau com uma incógnita
Chama –se equação do 2º grau na incógnita x, toda equação
que pode ser colocada na forma ax
2
+ bx + c = 0, em que a,
b e c são números reais e a ≠ 0.
Ex: 3x
2
+ 4x + 1 = 0
a = 3 ; b = 4 e c = 1
Equação completa e incompleta
Uma equação do 2º grau é completa quando b e c são diferentes de zero.
Exemplos:
x² - 9x + 20 = 0 e -x² + 10x - 16 = 0 são equações completas.
Uma equação do 2º grau é incompleta quando b ou c é igual a zero, ou ainda quando ambos são iguais a zero.
Exemplos:
|
|
|
Raízes de uma equação do 2º grau
Resolver uma equação do 2º grau significa determinar suas raízes.
| Raiz é o número real que, ao substituir a incógnita de uma equação, transforma-a numa sentença verdadeira. |
Resolução de equações incompletas
Utilizamos na resolução de uma equação incompleta as técnicas da fatoração.
Caso: Equação do tipo 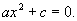
Exemplos:
Determine as raízes da equação 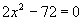 , sendo U = IR.
, sendo U = IR.
Solução:

De modo geral, a equação do tipo 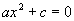 possui duas raízes reais se
possui duas raízes reais se 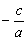 for um número positivo, não tendo raiz real caso
for um número positivo, não tendo raiz real caso 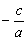 seja um número negativo.
seja um número negativo.
Exercícios que não resolveu
Página 39 exercício 6.
Não consegui fazer
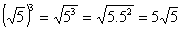
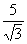
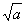 , pois
, pois