Multiplicação com radicais
Para multiplicar radicais, é preciso analisar em qual das situações abaixo os radicais se encontram.
Índices iguais
- Para a multiplicação de radicais, aplicamos a 3º propriedade.
Exemplos:
-raiz quinta de 4 vezes raiz quinta de 8 = raiz quinta de 4x8 = raiz quinta de 32 = raiz quinta de 2 = 2.
-raiz sexta de 2 elevado ao cubo x raiz sexta de 2 elevada à quarta potência =
raiz sexta de 2 elevado ao cubo x 2 elevado à quarta potência = raiz sexta de 2 elevada á sétima potência(porque somou-se o cubo x quarta potência) = raiz sexta de 2 elevada á sexta potência x 2 elevado á 1= 2 x raiz sexta de 2.
Índices diferentes
Exemplos:
-raiz quadrada de 6 dividido por raiz cúbica de 6
MMC(2, 3) = 6
raiz quadrada de 6 = 2x3(índices) raiz quadrada de 6, 1x3(índices) = raiz sexta de 6 elevado ao cubo
raiz cúbica de 6 = 3x2(índices) raiz sexta de 6, 1x2(índices) = raiz sexta de 6 elevado ao quadrado
Então: raiz quadrada de 6 dividido por raiz cúbica de 6 = raiz sexta de 6 elevado ao cubo dividido por raiz sexta de 6 elevado ao quadrado = raiz sexta de 6, 2-3(índices) = raiz sexta de 6.
Divisão de radicais
Índices iguais
-Para a divisão de radicais, aplicamos a 4º propriedade.
Exemplos:
raiz cúbica de 9 sobre raiz cúbica de 3 = raiz cúbica de 9 = raiz cúbica de 3.
3
Índices diferentes
Nesse caso, é necessário reduzir os radicais ao mesmo índice e, depois, efetuar a divisão, como no caso anterior.
Exemplos:
- raiz quadrada de 6 dividido por raiz cúbica de 6
MMC(2,3) = 6
raiz quadrada de 6 = 2x3 (índices) raiz de 6 elevado a 1x3 (índices) = raiz sexta de 6 elevado ao cubo
raiz cúbica de 6 = 3x2(índices) raiz de 6 elevado a 1x2(índices) = raiz sexta de 6 elevado ao quadrado
Então:raiz quadrada de 6 dividido por raiz cúbica de 6 = raiz sexta de 6 elevado ao cubo dividido por raiz sexta de 6 elevado ao quadrado = raiz sexta de 6 3-2 = raiz sexta de 6.
Principais dificuldades
No começo eu tive dificuldade em fazer os exercícios que cotiam números na frente de uma raiz como pro exemplo:(4raiz quadrada de 8 - 2raiz quadrada de 18)dividido por raiz cúbica de 2.
Potenciação com radicais
De modo geral, para se elevar um radical a um dado expoente, basta elevar o radicando àquele expoente.
Exemplos:
-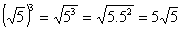
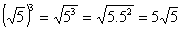
-(raiz quadrada de 5) elevado ao cubo = raiz quadrada de 5 levado ao cubo
Principais dificuldades
Minha principal dificuldade foi que tinha que recordar produtos notáveis.
Racionalização de Denominadores
Considere a fração: 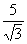 que seu denominador é um número irracional.
que seu denominador é um número irracional.
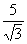 que seu denominador é um número irracional.
que seu denominador é um número irracional.Vamos agora multiplicar o numerador e o denominador desta fração por 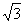 , obtendo uma fração equivalente:
, obtendo uma fração equivalente:
Observe que a fração equivalente 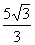 possui um denominador racional.
possui um denominador racional.
A essa transformação, damos o nome de racionalização de denomindores.
A racionalização de denominadores consiste, portanto, na obtenção de um fração com denominador racional, equivalente a uma anterior, que possuía um ou mais radicais em seu denominador.
Para racionalizar o denominador de uma fração devemos multiplicar os termos desta fração por uma expressão com radical, denominado fator racionalizante, de modo a obter uma nova fração equivalente com denominador sem radical.
Principais casos de racionalização:
1º Caso: O denominador é um radical de índice 2:
Exemplos:
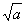 , pois
, pois 2º Caso: O denominador é um radical de índice diferente de 2.
Exemplos:
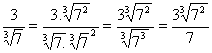
Principais dificuldades
No começo eu tive dificuldade em fazer certas operações como por exemplo:
o item F da página 37 exercício 2, que está escrito raiz quadrada de 11+1 sobre raiz quadrada de 11-1.
Nenhum comentário:
Postar um comentário